Sass et la trigonométrie

Il arrive parfois qu’on ait à travailler en Sass avec des triangles, des cercles ou des coordonnées 2D voire 3D. La trigonométrie s’invite alors avant même qu’on ne l’appelle, et les fonctions cosinus, sinus et tangente se rendent indispensables. Si vous utiliser une librairie comme Compass, vous avez déjà accès à ces fonctions ; l’objectif de cet article sera de créer ces fonctions de toutes pièces.

Les séries entières

Prenons pour commencer l’exemple de cosinus. Il existe trois manière de définir la valeur du cosinus d’un angle :

À l’aide d’un triangle

En considérant un triangle rectangle :

• contenant l’angle α,
• avec h la longueur de l’hypoténuse
• avec a la longueur de l’autre côté adjacent à α

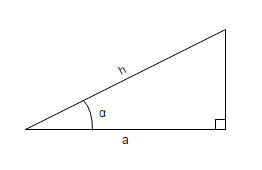
Nous avons cos(α) = a / h.

À l’aide d’un cercle

En considérant :

• un cercle de rayon 1
• la droite passant par l’origine du cercle et faisant un angle α avec son diamètre horizontal

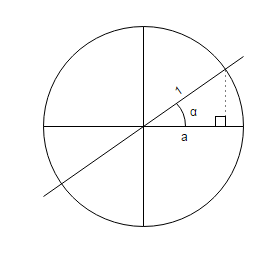
Il est alors possible de reproduire les calculs effectués avec un triangle. On peut voir ci-dessus qu’un triangle rectangle peut être tracé avec pour trois sommets :

• l’origine du cercle
• l’interaction entre la droite et le cercle
• la projection de cette intersection sur le diamètre horizontal du cercle

Nous avons cos(α) = a / h, soit cos(α) = a.

À l’aide des séries entières

L’inconvénient des deux précédentes méthodes, c’est qu’il nous manque des données : les longueurs des côtés h et a. Pour la méthode avec le cercle, on fixe arbitrairement h = 1, mais la longueur de a reste indéterminée. Sans informations supplémentaires, impossible donc de calculer un cosinus avec ces méthodes.

C’est là que la troisième méthode va trouver son intérêt, elle permet de calculer un cosinus à l’aide de la fonction suivante :

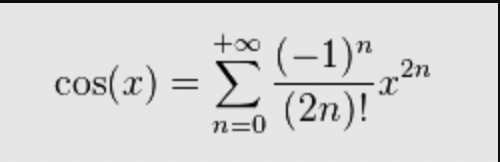
Ici, plus d’inconnues : nous connaissons x et n à tout instant. Il ne reste plus qu’à implémenter ce calcul en Sass, et à définir une limite de précision. La formule existe d’ailleurs aussi pour sinus :

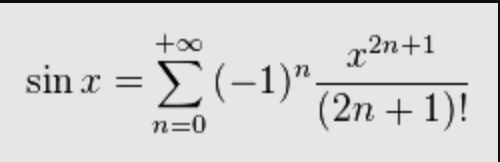
Nous aurons toutefois besoin d’encore quatre choses avant d’attaquer ces formules :

• la fonction puissance
• la fonction factorielle
• la valeur de pi
• une fonction pour passer des degrés en radians

Fonction puissance

La fonction puissance est assez simple à écrire. Pour xⁿ il s’agit juste de multiplier 1 par x, et ce n fois. Petite nuance toutefois, quand vous utilisez une puissance négative, il faut diviser au lieu de multiplier. Dans le cas où la puissance est nulle, on retournera toujours la valeur 1 :

@function pow($x, $n) {
  $pow: 1;
  @if $n > 0 {
    @for $i from 1 through $n {
      $pow: $pow * $x;
    }
  }
  @else if $n < 0 {
    @for $i from 1 through -$n {
      $pow: $pow / $x;
    }
  }
  @return $pow;
}

Fonction exponentielle

La fonction exponentielle n’est pas plus compliquée à écrire :

@function fact($n) {
  $fact: 1;
  @if $n > 0 {
    @for $i from 1 through $n {
      $fact: $fact * $i;
    }
  }
  @return $fact;
}

On notera que comme -5 n’est pas une entrée valide pour la fonction factorielle (qui n’accepte que les entiers naturels), il n’est pas nécessaire de gérer les entrées négatives. Ici, la fonction retournera la valeur 0 pour toute entrée négative, et 1 pour une entrée nulle.

Passer des degrés en radians

Les fonctions trigonométriques utilisent uniquement les radians. Comme nous utilisons généralement des angles en degrés, il est obligatoire d’avoir une fonction permettant de traduire ces degrés en radians.

On sait que 360° = 2π, ce qui permet par un produit en croix de déduire : deg2rad(α) = 2π * α / 360

@function pi() {
  @return 3.1415926535;
}
@function deg2rad($angle) {
  @if unit($angle) == deg {
    $angle: $angle / 1deg;
  }
  @return 2 * pi() * $angle / 360;
}

Utiliser une fonction plutôt qu’une variable pour retourner la valeur de pi est assez intéressant, car ainsi personne ne risque de modifier sa valeur par mégarde. Enfin, la condition dans la fonction sert uniquement à supprimer l’unité deg, pour vous permettre d’utiliser indifféremment deg2rad(45) et deg2rad(45deg).

Cosinus

Ça y est, nous avons tous les outils nécessaires à la création de la fonction cosinus. Voici du coup le résultat ci-dessous :

@function cos($angle) {
  $cos: 0;
  @for $i from 0 through 10 {
    $cos: $cos + (pow(-1, $i) / fact(2 * $i)) * pow($angle, 2 * $i);
  }
  @return $cos;
}

Comme la fonction cosinus n’accepte que les radians, il faudra penser à utiliser la fonction deg2rad() dès que nécessaire :

$a: cos( deg2rad(150) );    // -0.8660254
$a: cos( deg2rad(150deg) ); // -0.8660254
$a: cos( 5 * pi() / 6 );    // -0.8660254

Actuellement, la boucle @for est utilisée 10 fois. Augmenter cette valeur i augmenterait la précision, tout en réduisant la vitesse de compilation, il est donc important de fixer une valeur i assez basse pour ne pas passer 3 heures à compiler, mais suffisamment haute pour ne pas perdre en précision. Sur tous les tests que j’ai pu effectuer, j’obtiens les mêmes résultats pour toute valeur i supérieure ou égale à 8 ; on peut donc fixer i à 10, histoire d’avoir une petite marge de sécurité.

Sinus

Même fonctionnement pour la fonction sinus, que voici ci-dessous :

@function sin($angle) {
  $sin: 0;
  @for $i from 0 through 30 {
    $sin: $sin + (pow(-1, $i) / fact(2 * $i + 1) ) * pow($angle, (2 * $i + 1));
  }
  @return $sin;
}

Tangente

La tangente étant simplement définie par tan(α) = sin(α) / cos(α), on peut facilement réutiliser les fonctions précédentes :

@function tan($angle) {
  @return sin($angle) / cos($angle);
}

Liens

• Définition de cosinus à partir des séries entières
• Définition de sinus à partir des séries entières
• Fonctions mathématiques de Compass